Lab 06: BSTMap
FAQ
The FAQ for this lab can be found here.
Introduction
In this lab, you’ll create BSTMap, a BST-based implementation of the Map61B
interface, which represents a basic tree-based map. You will be creating this
completely from scratch, using the interface provided as your guide.
After you’ve completed your implementation, you’ll compare the performance of
your implementation to a list-based Map implementation ULLMap as well as the
built-in Java TreeMap class (which uses a BST variant known as a red-black tree).
Pulling from skeleton
To get the assignment, pull from the skeleton in your personal repository:
git pull skeleton main
This assignment is lab06.
BSTMap
In this lab (and future labs), we may not provide as much skeleton code as in the past. If you’re having trouble getting started, please come in to lab or check out any of the resources provided!
Create a class BSTMap that implements the Map61B interface using a BST
(Binary Search Tree) as its core data structure. Your code will not compile until
you create the BSTMap class and implement all the methods in Map61B.
You can implement methods one at a time by writing the method signatures
of all the required methods, but throwing UnsupportedOperationExceptions
for the other implementations until you get around to actually writing them.
Refer to this section on how to throw the exception.
In your implementation, you should ensure that generic keys K in BSTMap<K,V>
implement
Comparable.
This is called a bounded type parameter.
The syntax
is a little tricky, but we’ve given an example below. Here, we are creating
a BSTSet for Comparable objects. We’ve included the rather strange
compareRoots for pedagogical purposes (for a compareTo refresher, see this
documentation):
public class BSTSet<K extends Comparable<K>> implements Set61B<K> {
private class BSTNode {
K item;
// ...
}
private BSTNode root;
/* Returns whether this BSTSet's root is greater than, equal to, or less
* than the other BSTSet's root, following the usual `compareTo`
* convention. */
public int compareRoots(BSTSet other) {
/* We are able to safely invoke `compareTo` on `n1.item` because we
* know that `K` extends `Comparable<K>`, so `K` is a `Comparable`, and
*`Comparable`s must implement `compareTo`. */
return this.root.item.compareTo(other.root.item);
}
// ...
}
You may have noticed that the syntax for a bounded type parameter uses extends
even though Comparable is an interface. In the context of bounded type
parameters, extends can mean extends or implements
(docs). Don’t ask us why - we don’t know either.
(The syntax also implies you can “extend” final classes such as Integer,
which is impossible. Go Java!)
Remember, the code snippet above emulates a Set - you’ll need to implement a
Map. We recommend you use similar logic for BSTMap, with some nested node
class to help facilitate your implementation. Your BSTMap should have two
generic parameters K and V, representing the generic types of the keys and
values in your BSTMap, respectively.
IntelliJ has a nice feature that will generate the method signatures for you. If
you’re implementing an interface and haven’t implemented all the methods,
IntelliJ will highlight the class signature in red. If you hover over this, you
should be able to select Implement methods. On the pop-up window, make sure you’ve
selected the option for “Copy JavaDoc” and “Insert @Override”. Click “OK”
and IntelliJ should populate the class with the required method signatures
(they won’t be functional though!) and copy over the comments.
It should look something like this (you don’t have Set61B, this is just an
example!):

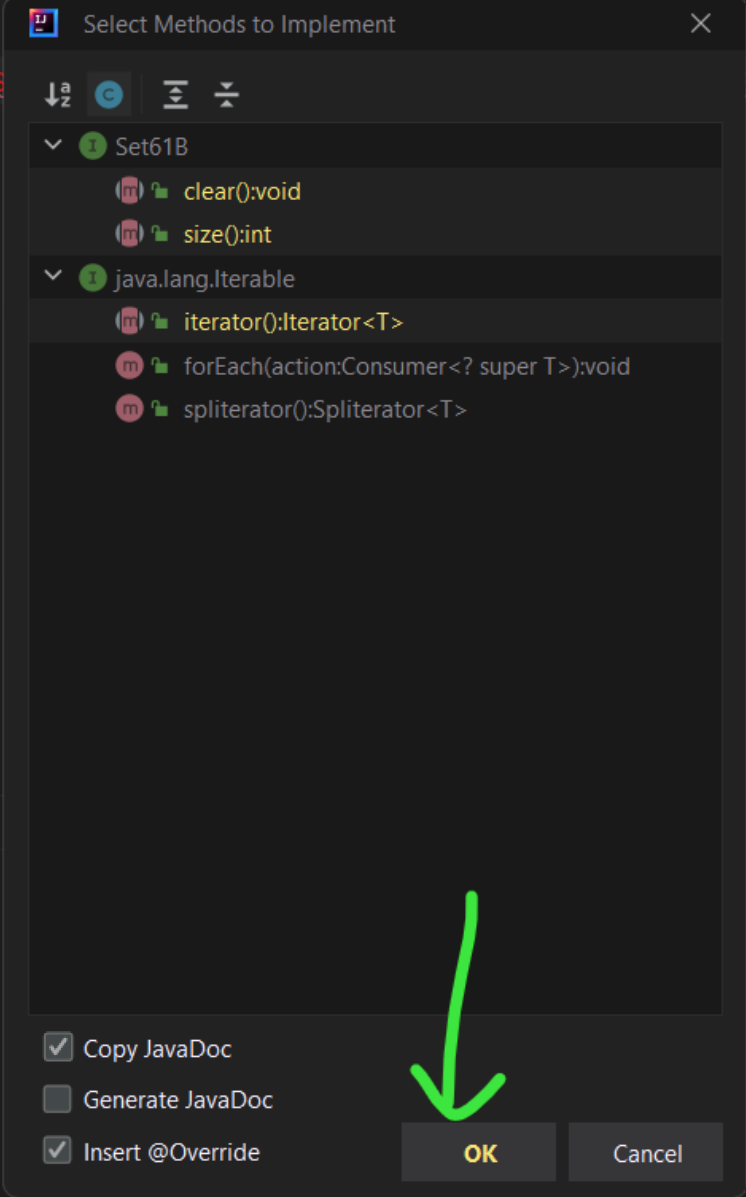
In this example, IntelliJ will generate the clear, size, and iterator
method signatures, because that’s all our mythical Set61B interface
requires. If you follow this procedure with your code, you should have all the
method signatures required for Map61B. (You can also pick and choose
which signatures to generate, if you’d like.)
Exercise: BSTMap
As mentioned, you’ll want to create a class, BSTMap, that implements the Map61B interface.
Make sure you are writing your implementation in BSTMap.java, otherwise your code might not
run on the autograder! The following methods are required:
void put(K key, V value): Associates the specifiedkeywith thevalue.V get(K key): Returns the value that is associated withkey.boolean containsKey(K key): Returns if this map has a mapping for the givenkey.int size(): Returns the number of key-value mappings.void clear(): Removes every mapping from this map.
Make sure to read through the comments for each method in the Map61B interface
to fully understand what to implement. The above descriptions are not necessarily
comprehensive.
For debugging purposes, your BSTMap should also include an additional method
printInOrder() (not given in the Map61B interface) that prints out your
BSTMap in order of increasing Key. We will not test the result of this method,
but you may find this helpful for testing your implementation!
Implement the BSTMap class, which implements the Map61B interface
and the associated, non-optional methods. You should ensure that the keys in
your BSTMap are Comparable by using a bounded type parameter.
We strongly recommend you create helper methods to facilitate your implementation
(specifically, recursive helper methods are strongly encouraged).
Unfortunately, most methods you need to implement rely on others for testing
purposes (get requires put, etc.). This makes it difficult to test most methods until
you implement put. We recommend you implement the methods in the order
specified in Map61B.
You can test your implementation
using TestBSTMap.java.
There is an optional part of BSTMap. These methods are optional to implement:
iterator, remove, keySet. They are not required for the timing portion, described in this
section.
As mentioned, if you are not implementing the optional part, throw an
UnsupportedOperationException, like below:
throw new UnsupportedOperationException();
If you are completing the optional part, refer to this
section
and the comments in Map61B for a more detailed description.
Resources
The following resources might prove useful:
- Lecture 16 slides.
ULLMap.java(given insrc/), an unordered, linked-list-basedMap61Bimplementation.- To help you also get started, an algorithmic guide to
putandgetcan be found here
So… How Fast Is It?
There is one interactive speed test provided in InsertRandomSpeedTest.java.
Do not attempt to run this test before you’ve completed BSTMap.
Once you’re ready, you can run the tests in IntelliJ.
The InsertRandomSpeedTest class performs tests on element-insertion speed of
your BSTMap, ULLMap (provided), Java’s built-in TreeMap, and Java’s
built-in HashMap (which you’ll explore more in a later lab). It works by
asking the user for a desired length of each String to insert, and also for an
input size (the number of insertions to perform). It then generates that many
Strings of length as specified and inserts them into the maps as
<String, Integer> pairs.
Try it out and see how your data structure scales with the number of insertions
compared to the naive and industrial-strength implementations. Remember that
asymptotics aren’t representative on small samples, so make sure your inputs
are sufficiently large if you are getting a confusing trend (keep in mind that there
is a limit thought - if you enter too large of a value, the program might overflow,
so play around with sufficiently large values). Record your results
in a file named speedTestResults.txt.
Run the speed tests and record your results in speedTestResults.txt.
There is no standard format required for your results, but at a minimum, you
should include what you did and what you observed.
Scoring
The lab is out of 5 points. There are no hidden tests on Gradescope, in the sense that
the score you get on Gradescope is your final score. However, there is one test not provided
locally, which checks for your speedTestResults.txt. Passing the local test TestBSTMap.java
means that you will get full credit for BSTMap.java, but not necessarily for your speedTestResults.txt
on Gradescope. So, for this lab, as long as you pass the relevant local tests (TestBSTMap.java) and
fill out the speedTestResults.txt file sufficiently, you will get full credit on Gradescope.
More (Ungraded) Exercises for BSTMap
These will not be graded, but you can still receive feedback using the local
tests, specifically TestBSTMapExtra.java (and on the autograder).
Implement the methods iterator(), keySet(), remove(K key) in your BSTMap
class. When implementing the iterator method, you should return an iterator
over the keys, in sorted order. remove() is fairly
challenging - you’ll need to implement Hibbard deletion.
For remove, you should return null if the argument key does not exist in the
BSTMap. Otherwise, delete the key-value pair (key, value) and return value.
Submission
Just as you did for the previous assignments, add, commit, then push your Lab 06 code to GitHub. Then, submit to Gradescope to test your code.
Optional: Asymptotics Problems
This part is also optional, and we’ve included it here for additional practice on asymptotics. Check your answers against the solutions!
Given B, a BSTMap with N key-value pairs, and (K, V), a random key-value pair, answer the following questions.
Unless otherwise stated, “big-Oh” bounds (e.g. $\mathcal{O}(N)$) and “big-Theta” bounds (e.g. $\Theta(N)$) refer to the number of comparisons in the given method call(s).
For questions 1-7, state whether the statement is true or false. For question 8, give a runtime bound.
B.put(K, V)$\in \mathcal{O}(\log N)$B.put(K, V)$\in \Theta(\log N)$B.put(K, V)$\in \Theta(N)$B.put(K, V)$\in \mathcal{O}(N)$B.put(K, V)$\in \mathcal{O}(N^2)$
- For a fixed key
Cnot equal toK, bothB.containsKey(C)andB.containsKey(K)run in $\Omega(\log N).$ - (This question is quite difficult.) Let
bbe aNodeof aBSTMap, and two subtrees rooted atroot, calledleftandright. Further, assume the methodnumberOfNodes(Node p)returns the number of nodes ($M$) of the subtree rooted atpand runs in $\Theta(M)$ time. What is the running time, in both the worst and best case, ofmystery(b.root, z), assuming1 <= z < numberOfNodes(b.root)?
Hint: See if you can work out what mystery does first, then see how it accomplishes it.
public Key mystery(Node b, int z) {
int numLeft = numberOfNodes(b.left);
if (numLeft == z - 1) {
return b.key;
} else if (numLeft > z) {
return mystery(b.left, z);
} else {
return mystery(b.right, z - numLeft - 1);
}
}